米国はPodcastの番組が豊富で、デーティングサービスのTinderの番組も配信されています。恋愛、婚活ネタ好きとしては外せないので、通勤中に聞いていたところ、出てきたのが、「デートを繰り返しても、なかなか1人に決められない！」という今っぽい問題。デーディングサービスにより、出会えすぎてしまう昨今、「もっといい人に会えるかも？」と思ってしまい、なかなか1人に落ち着くことができない状態に陥ってしまう人も多いようです。

そしてこれには、Secretary Problemという名前がついているようで、気になってみたので、詳しく調べてみました。

Secretary Problem＝秘書問題？

なぜSecretary？秘書？と思い調べてみたところ、日本語のWikiにも「秘書問題」という項目がありました。

数学の世界では、一定の条件の下での、最良選択をどのように行うべきかの研究が行われており、簡単な例ではシンプルな結論も得られている。（中略）

「秘書問題」は、しばしば「結婚問題」や「最良選択問題」等幅広くいろいろな呼び方をされているものである。

最初のいくつかの選択肢を見送った後、それらの選択肢との比較に基づく一定の基準に従って、最終的な選択を行うという典型的な「最適停止問題」のケースとなっている。

ベスト・ベターな秘書をどうやって選んだらよいのか－「秘書問題」で効率的な選択を実現する－ [ニッセイ基礎研究所の記事より]

秘書の採用プロセスで「最良の応募者を採用する確率を最大にする」にはどうしたらよいのか？という問題がベースになっており、これが恋愛＆結婚にも当てはめることができるため、デーティングや結婚相手を決めるシチュエーションでもSecretary Problemという言葉が利用されているようです。

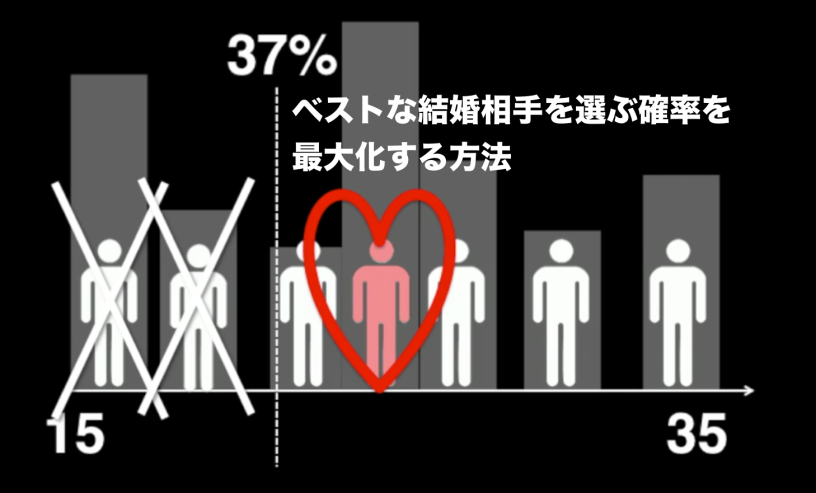
ベストな結婚相手を選ぶ確率を最大化する方法

それにしても、ベストな結婚相手を選ぶ確率を最大化する方法があるなんて知ってました！？あくまで確率の話ではありますが、これは詳しく知っておきたい！（結婚してるけど）ということで色々調べたところ、Washington Postにわかりやすい記事がありました。

英語が得意な方はこちらのWashington Postの記事「When to stop dating and settle down, according to math」をどうぞ。またTED Talk「The mathematics of love」でも「数学的に使える愛のTips」として解説されていました。下記は、TED Talkの画像を使わせてもらいながら解説します。

マジックナンバーは37%！

以下を前提条件とします。

1. ベストな結婚相手を見つけたい
2. 人生で結婚相手を見つけるまでに付き合える人（N）の人数は限られている（Nは人によって異なる）
3. N人には優劣があり、複数の人が同じ順位になることはない（1位からN位まで重複無く順位付けできる）
4. 優劣関係なく、無作為な順序で1人ずつお付き合いする。次に誰と付き合うかは常に同じ確率である。
5. 一定期間付き合った後、結婚するか・別れるかの判断をするものとする
6. その人と結婚するかは、それまで付き合った人との相対的順位にのみ基づいて決定する
7. 一度別れた人とよりを戻すことはできない
8. こちらが結婚を決めたら相手は決して断らない
9. このような状況で、最良の結婚相手を選択することが問題の目的である

さて、その「最良の結婚相手を選択する」確率を最大化する方法ですが、

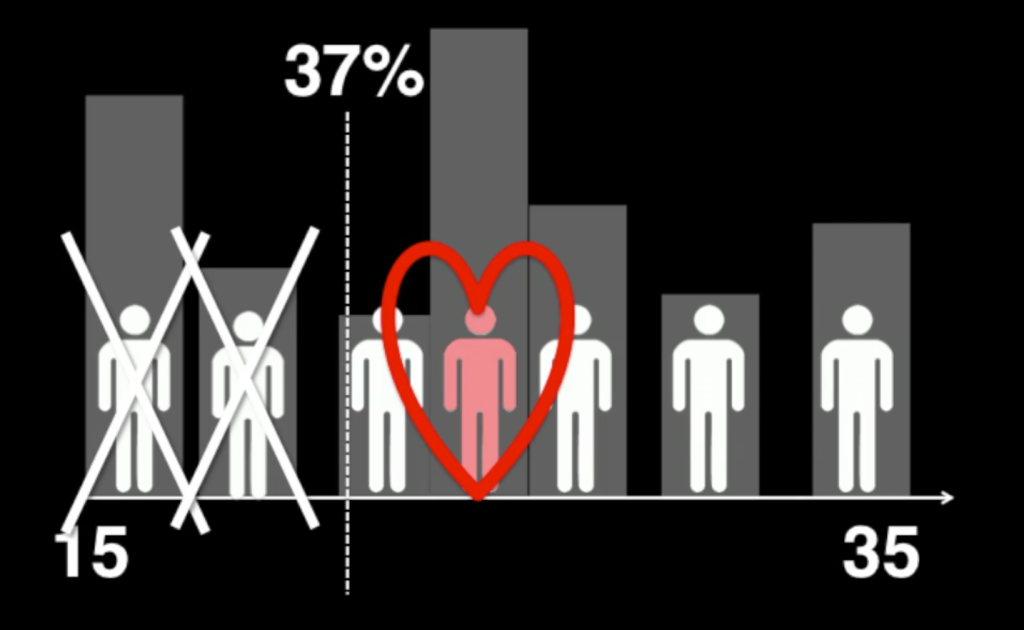
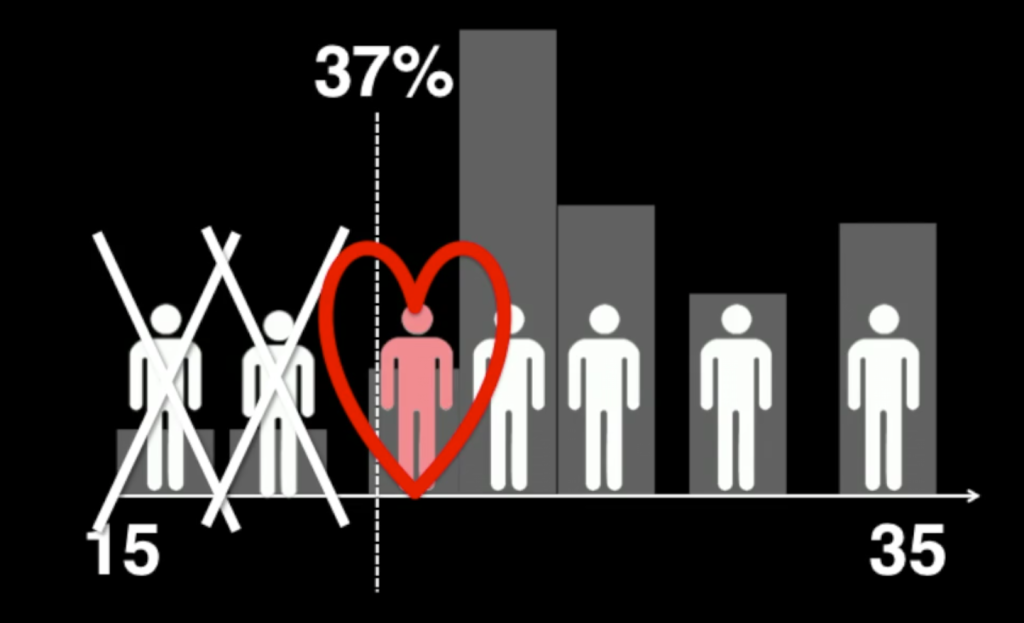
• 付き合える人数の全N人の37%までお付き合いします。この37%とは結婚しません。
• 37%を超えたところから結婚相手探しをはじめます。
• 最初の37%の人より結婚相手として優れている人と知り合ったら、その人と結婚します。
• 全N人に満たなくても、そこで婚活は終了です。

そうすると、ランダムに結婚相手を選んだ場合に「最良の結婚相手を選択する」確率が9%なのに対して、この方法に従うと、「最良の結婚相手を選択する」確率が37%まで上がるんだそうです。

あれ、意外と低い！？けど、9%と37%だったら、37%の方法を選びたくないですか！？

もちろんリスクもあります

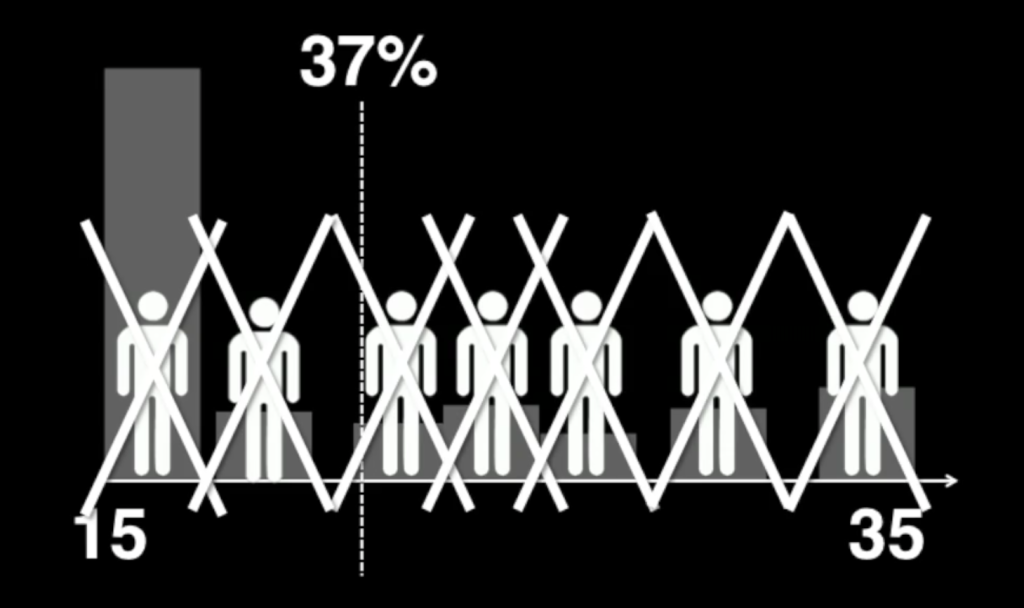
また最初の37%のレベルが低かった場合、その次に来た人がまあまあでも選ぶことになってしまうため、ベストな人にたどり着けないまま終わってしまう可能性もあります。

もちろん、最初の37%にベストな人が含まれてしまう可能性もあり、結果誰とも結婚せずに終わるかもしれません。

Washington Postの記事によると、微妙にチューニングすることも可能なようで、37%ではなく30%にした場合は、「this version means that you end up dating around a little less and selecting a partner a little sooner. But you have a higher chance of ending up with someone who is pretty good, and a lower chance of ending up alone.」ということで、ベストではないけれども良い感じの人を選択できる可能性が高まり、かつ最後まで1人という可能性が低くなるそうです。難しいけど、面白い。

30歳までにベストな人と結婚するためには？

あくまで確率論の話ですが、具体的な年齢で考えてみたくなりませんか！？
ということで実際の数字を入れて考えてみると、

• 30歳までは結婚したい
• 18歳から30歳まで、12年間は結婚を意識したお付き合いをする
• 1人と1年間お付き合いするとして、最大お付き合いできる人数は12人
• 12人の37%＝4.44人≒4人とすると、4人までは基準作りのお付き合いとなる
• 5人目からは本当の意味での結婚相手探しがはじまる
• 5人目以降で最初の4人よりいい相手が見つかったら結婚する

18歳から1年ずつ付き合って5人目ということは、23歳ぐらいからきちんと身構えてないといけないではないですか！意外とはやめから心の準備が必要みたいです。

付き合える最大人数を3人で考えるとわかりやすい

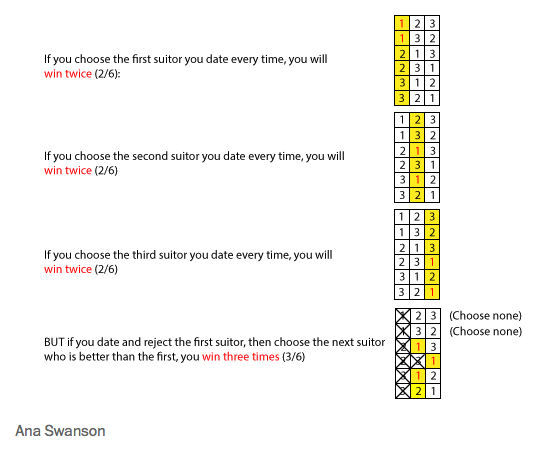
前述のWashington Postの記事の中に、付き合える最大人数を3人にした場合の確率図があります。

• これから3人の人とお付き合いできる可能性がある
• 3人には1位、2位、3位という明確な優劣があるとする
• その中から結婚相手を選ぶ
• 1位、2位、3位の人と付き合う順番はランダム
• 1位を選びたい

という条件だとすると以下の組み合わせが出てきます。順列組み合わせの問題みたいですが、

最初にお付き合いした人で決める場合、1位の人を選択できる確率は2/6＝33%
2番目にお付き合いした人で決める場合、1位の人を選択できる確率は2/6＝33%
3番目にお付き合いした人で決める場合、1位の人を選択できる確率は2/6＝33%
1番目にお付き合いした人を基準とし、その次にそれを上回る人を選んだ場合に1位の人を選択できる確率は、3/6なので50%

確率があがっている！

まあでも現実はそうもいかない

まあとはいえ、前提条件がなかなか難しいですよね。

「一定期間付き合った後、結婚するか・別れるかの判断をするものとする」…なかなか決められなくてズルズルしちゃったりしますし。

「その人と結婚するかは、それまで付き合った人との相対的順位にのみ基づいて決定する」…いやいや、必ずしも相対的順位が付けられるものではないし。この人にも、あの人にもそれぞれ比べられない良い所があるのよ。

「一度別れた人とよりを戻すことはできない」…意外とがんばってよりを戻そうとしたりしちゃったり。

「こちらが結婚を決めたら相手は決して断らない」…こちらが決めても相手がその気じゃないこともありますし。。

ということで、まああくまで参考程度の話ですが、なんか面白かったのでブログにまとめてみました。

TED Talk「The mathematics of love」ではこの他にも「数学的に使える愛のTips」が2つ紹介されていたので、興味がある方は動画を見てみてください。